La programación lineal es un procedimiento o algoritmo matemático mediante el cual se resuelve un problema indeterminado, formulado a través de un sistema de inecuaciones lineales, optimizando la función objetivo, también lineal.

Consiste en optimizar (minimizar o maximizar) una función lineal, denominada función objetivo, de tal forma que las variables de dicha función estén sujetas a una serie de restricciones que expresamos mediante un sistema de inecuaciones lineales.

VARIABLES

Las variables son números reales mayores o iguales a cero. 

En caso que se requiera que el valor resultante de las variables sea un número entero, el procedimiento de resolución se denomina Programación entera.

RESTRICCIONES

Las restricciones pueden ser de la forma:

Tipo 1: 

Tipo 2: 

Tipo 3: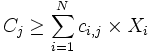 

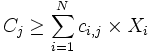
Donde:

• A = valor conocido a ser respetado estrictamente;
• B = valor conocido que debe ser respetado o puede ser superado;
• C = valor conocido que no debe ser superado;
• j = número de la ecuación, variable de 1 a M (número total de restricciones);
• a; b; y, c = coeficientes técnicos conocidos;
• X = Incógnitas, de 1 a N;
• i = número de la incógnita, variable de 1 a N.

En general no hay restricciones en cuanto a los valores de N y M. Puede ser N = M; N > M; ó, N < M.

Sin embargo si las restricciones del Tipo 1 son N, el problema puede ser determinado, y puede no tener sentido una optimización.

Los tres tipos de restricciones pueden darse simultáneamente en el mismo problema.